Extracting and Depositing Bits
Suppose you have a 64-bit word and wish to extract a couple bits from it.
For example you just performed a SWAR
algorithm and wish to extract the least significant bit of each byte in the u64.
This is simple enough, you simply perform a binary AND with a mask of
the bits you wish to keep:
let out = word & 0x0101010101010101;
However, this still leaves the bits of interest spread throughout the 64-bit word. What if we also want to compress the 8 bits we wish to extract into a single byte? Or what if we want the inverse, spreading the 8 bits of a byte among the least significant bits of each byte in a 64-bit word?
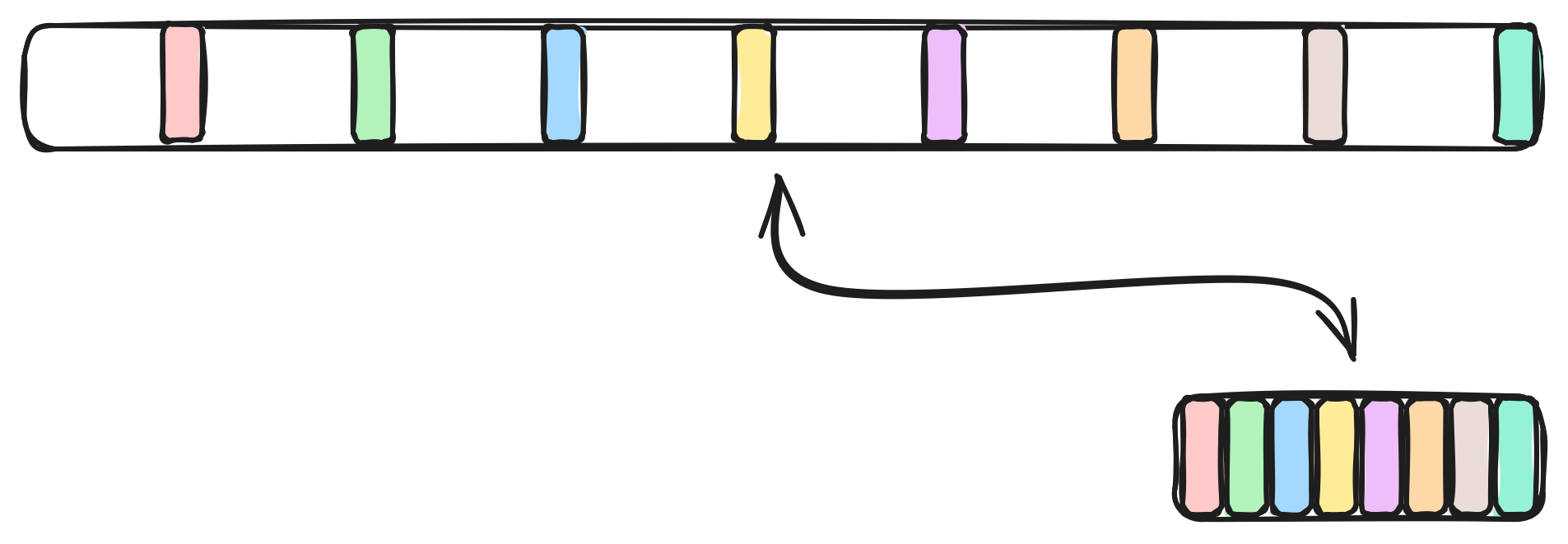
PEXT and PDEP
If you are using a modern x86-64 CPU, you are in luck. In the much underrated
BMI instruction
set there
are two very powerful instructions: PDEP and PEXT. They are inverses of each
other, PEXT extracts bits, PDEP deposits bits.
PEXT takes in a word and a
mask, takes just those bits from the word where the mask has a 1 bit, and
compresses all selected bits to a contiguous output word. Simulated in Rust
this would be:
fn pext64(word: u64, mask: u64) -> u64 {
let mut out = 0;
let mut out_idx = 0;
for i in 0..64 {
let ith_mask_bit = (mask >> i) & 1;
let ith_word_bit = (word >> i) & 1;
if ith_mask_bit == 1 {
out |= ith_word_bit << out_idx;
out_idx += 1;
}
}
out
}
For example if you had the bitstring abcdefgh and mask 10110001 you would
get output bitstring 0000acdh.
PDEP is exactly its inverse, it takes contiguous data bits as a word, and
a mask, and deposits the data bits one-by-one (starting at the least significant
bits) into those bits where the mask
has a 1 bit, leaving the rest as zeros:
fn pdep64(word: u64, mask: u64) -> u64 {
let mut out = 0;
let mut input_idx = 0;
for i in 0..64 {
let ith_mask_bit = (mask >> i) & 1;
if ith_mask_bit == 1 {
let next_word_bit = (word >> input_idx) & 1;
out |= next_word_bit << i;
input_idx += 1;
}
}
out
}
So if you had the bitstring abcdefgh and mask 10100110 you would get output
e0f00gh0 (recall that we traditionally write bitstrings with the least
significant bit on the right).
These instructions are incredibly powerful and flexible, and the amazing thing is that these instructions only take a single cycle on modern Intel and AMD CPUs! However, they are not available in other instruction sets, so whenever you use them you will also likely need to write a cross-platform alternative.
Extracting bits with multiplication
While the following technique can’t replace all PEXT cases, it can be quite
general. It is applicable when:
- The bit pattern you want to extract is static and known in advance.
- If you want to extract $k$ bits, there must at least be a $k-1$ gap between two bits of interest.
We compute the bit extraction by adding together many left-shifted copies of
our input word, such that we construct our desired bit pattern in the uppermost
bits. The trick is to then realize that w << i is equivalent to w * (1 << i)
and thus the sum of many left-shifted copies is equivalent to a single
multiplication by (1 << i) + (1 << j) + ...
I think the technique is best understood by visual example. Let’s use our example from earlier, extracting the least significant bit of each byte in a 64-bit word. We start off by masking off just those bits. After that we shift the most significant bit of interest to the topmost bit of the word to get our first shifted copy. We then repeat this, shifting the second most significant bit of interest to the second topmost bit, etc. We sum all these shifted copies. This results in the following (using underscores instead of zeros for clarity):
mask = _______1_______1_______1_______1_______1_______1_______1_______1
t = w & mask
t = _______a_______b_______c_______d_______e_______f_______g_______h
t << 7 = a_______b_______c_______d_______e_______f_______g_______h_______
t << 14 = _b_______c_______d_______e_______f_______g_______h______________
t << 21 = __c_______d_______e_______f_______g_______h_____________________
t << 28 = ___d_______e_______f_______g_______h____________________________
t << 35 = ____e_______f_______g_______h___________________________________
t << 42 = _____f_______g_______h__________________________________________
t << 49 = ______g_______h_________________________________________________
t << 56 = _______h________________________________________________________
sum = abcdefghbcdefgh_cdefh___defgh___efgh____fgh_____gh______h_______
Note how we constructed abcdefgh in the topmost 8 bits, which we can then
extract using a single right-shift by $64 - 8 = 56$ bits. Since
(1 << 7) + (1 << 14) + ... + (1 << 56) = 0x102040810204080 we get the
following implementation:
fn extract_lsb_bit_per_byte(w: u64) -> u8 {
let mask = 0x0101010101010101;
let sum_of_shifts = 0x102040810204080;
((w & mask).wrapping_mul(sum_of_shifts) >> 56) as u8
}
Not as good as PEXT, but three arithmetic instructions is not bad at all.
Depositing bits with multiplication
Unfortunately the following technique is significantly less general than the previous one. While you can take inspiration from it to implement similar algorithms, as-is it is limited to just spreading the bits of one byte to the least significant bit of each byte in a 64-bit word.
The trick is similar to the one above. We add 8 shifted copies of
our byte which once again translates to a multiplication. By choosing a shift
that increases in multiples if 9 instead of 8 we ensure that the bit pattern
shifts over by one position in each byte. We then mask out our bits of interest,
and finish off with a shift and byteswap (which compiles to a single instruction bswap
on Intel or rev on ARM) to put our output bits on the least significant bits
and reverse the order.
This technique visualized:
b = ________________________________________________________abcdefgh
b << 9 = _______________________________________________abcdefgh_________
b << 18 = ______________________________________abcdefgh__________________
b << 27 = _____________________________abcdefgh___________________________
b << 36 = ____________________abcdefgh____________________________________
b << 45 = ___________abcdefgh_____________________________________________
b << 54 = __abcdefgh______________________________________________________
b << 63 = h_______________________________________________________________
sum = h_abcdefgh_abcdefgh_abcdefgh_abcdefgh_abcdefgh_abcdefgh_abcdefgh
mask = 1_______1_______1_______1_______1_______1_______1_______1_______
s & msk = h_______g_______f_______e_______d_______c_______b_______a_______
We once again note that the sum of shifts can be precomputed as 1 + (1 << 9) + ... + (1 << 63) = 0x8040201008040201, allowing the following implementation:
fn deposit_lsb_bit_per_byte(b: u8) -> u64 {
let sum_of_shifts = 0x8040201008040201;
let mask = 0x8080808080808080;
let spread = (b as u64).wrapping_mul(sum_of_shifts) & mask;
u64::swap_bytes(spread >> 7)
}
This time it required 4 arithmetic instructions, not quite as good as PDEP,
but again not bad compared to a naive implementation, and this is cross-platform.