Bitwise Binary Search: Elegant and Fast
I recently read the article Beautiful Branchless Binary Search by Malte Skarupke. In it they discuss the merits of the following snippet of C++ code implementing a binary search:
template<typename It, typename T, typename Cmp>
It lower_bound_skarupke(It begin, It end, const T& value, Cmp comp) {
size_t length = end - begin;
if (length == 0) return end;
size_t step = bit_floor(length);
if (step != length && comp(begin[step], value)) {
length -= step + 1;
if (length == 0) return end;
step = bit_ceil(length);
begin = end - step;
}
for (step /= 2; step != 0; step /= 2) {
if (comp(begin[step], value)) begin += step;
}
return begin + comp(*begin, value);
}
Frankly, while the ideas behind the algorithm are beautiful, I find the implementation complex and hard to understand or prove correct. This is not meant as a jab at Malte Skarupke, I find almost all binary search implementations hard to understand or prove correct.
In this article I will provide an alternative implementation based on similar ideas but with a very different interpretation that is (in my opinion) incredibly elegant and clear to understand, at least as far as binary searches go. The resulting implementation also saves a comparison in almost every case and ends up quite a bit smaller.
A brief history lesson
Feel free to skip this section if you are not interested in history, but I had to find out whose shoulders we are standing on. This is not only to give credit where credit is due, but also to see if any useful details were lost in translation.
Malte Skarupke says they learned about the above algorithm from Alex Muscar in their blog post. Alex says they found the algorithm while reading Jon L. Bentley’s book Writing Efficient Programs (ISBN 0-13-970244-X). Jon Bentley writes:
If we need more speed then we should consult Knuth’s [1973] definitive treatise on searching. Section 6.2.1 discusses binary search, and Exercise 6.2.1-11 describes an extremely efficient binary search program; […]
I own the referenced book hardcopy, Donald Knuth’s The Art of Computer Programming (also known as TAOCP), volume 3 Sorting and Searching. Exercise 6.2.1-11 is not the correct exercise in my edition, but 12 and 13 are, which are exercises referring to “Shar’s method”.
We have to scan chapter 6.2.1 to find the mentioned method. Finally, we find it on page 416. First as context, Knuth uses the following notation for binary search:
Algorithm U (Uniform binary search). Given a table of records $R_1, R_2, \dots, R_N$ whose keys are in increasing order $K_1 < K_2 < \cdots < K_N$, this algorithm searches for a given argument $K$. If $N$ is even, the algorithm will sometimes refer to a dummy key $K_0$ that should be set to $-\infty$. We assume that $N \geq 1$.
Now we can finally see Shar’s method:
Another modification of binary search, suggested in 1971 by L. E. Shar, will be still faster on some computers, because it is uniform after the first step, and it requires no table. The first step is to compare $K$ with $K_i$, where $i = 2^k$, $k = \lfloor \lg N\rfloor$. If $K$ < $K_i$, we use a uniform search with the $\delta$‘s equal to $2^{k-1}, 2^{k-2}, \dots, 1, 0$. On the other hand, if $K > K_i$ we reset $i$ to $i’ = N + 1 - 2^l$ where $l = \lceil\lg(N - 2^k + 1)\rceil$, and pretend that the first comparison was actually $K > K_{i’},$ using a uniform search with the $\delta$’s equal to $2^{l-1}, 2^{l-2}, \dots, 1, 0$.
The $\delta$’s the first paragraph refers to can be understood as the ‘step’ variable in the above C++ code. Overall Skarupke’s C++ code seems a fairly faithful implementation of Shar’s method as described by Knuth, except that Knuth uses one-based indexing which Skarupke’s method does not take into account. Knuth goes on to describe that Shar’s method never makes more than $\lfloor \lg N \rfloor + 1$ comparisons, which is one more than the minimum possible number of comparisons.
To finish the history lesson, I did look on Google Scholar, but I could not find a 1971 paper by L. E. Shar. I assume the modification was described in private communication with Knuth.
Lower bounds
Let us assume that we have a zero-indexed array $A$ of length $n$ that is in ascending order: $A[0] \leq A[1] \leq \cdots \leq A[n-1]$. We want to find the lower bound of some element $x$ in this array. This is the leftmost position we could insert $x$ into the array while keeping it sorted. Alternatively phrased, this is the number of elements strictly less than $x$ in the array.
A traditional binary search algorithm finds this number by keeping a range of possible solutions, repeatedly cutting that range in two pieces and selecting the only piece which contains the solution. This tends to be tricky to get right, as you must avoid overflows while computing the midpoint, and are dealing with multiple boundary conditions, both in your code as well as in your correctness invariant.
Before we begin with our solution that avoids this, we have to take a moment and
understand an important aspect of binary search. With each comparison we can
distinguish between two sets of outcomes. Thus with $k$ comparisons, we can
distinguish between $2^k$ total outcomes. However, for $n$ elements, there are
$n+1$ outcomes! For example, for an array of 7 elements there are 8 positions in
which $x$ could be sorted: 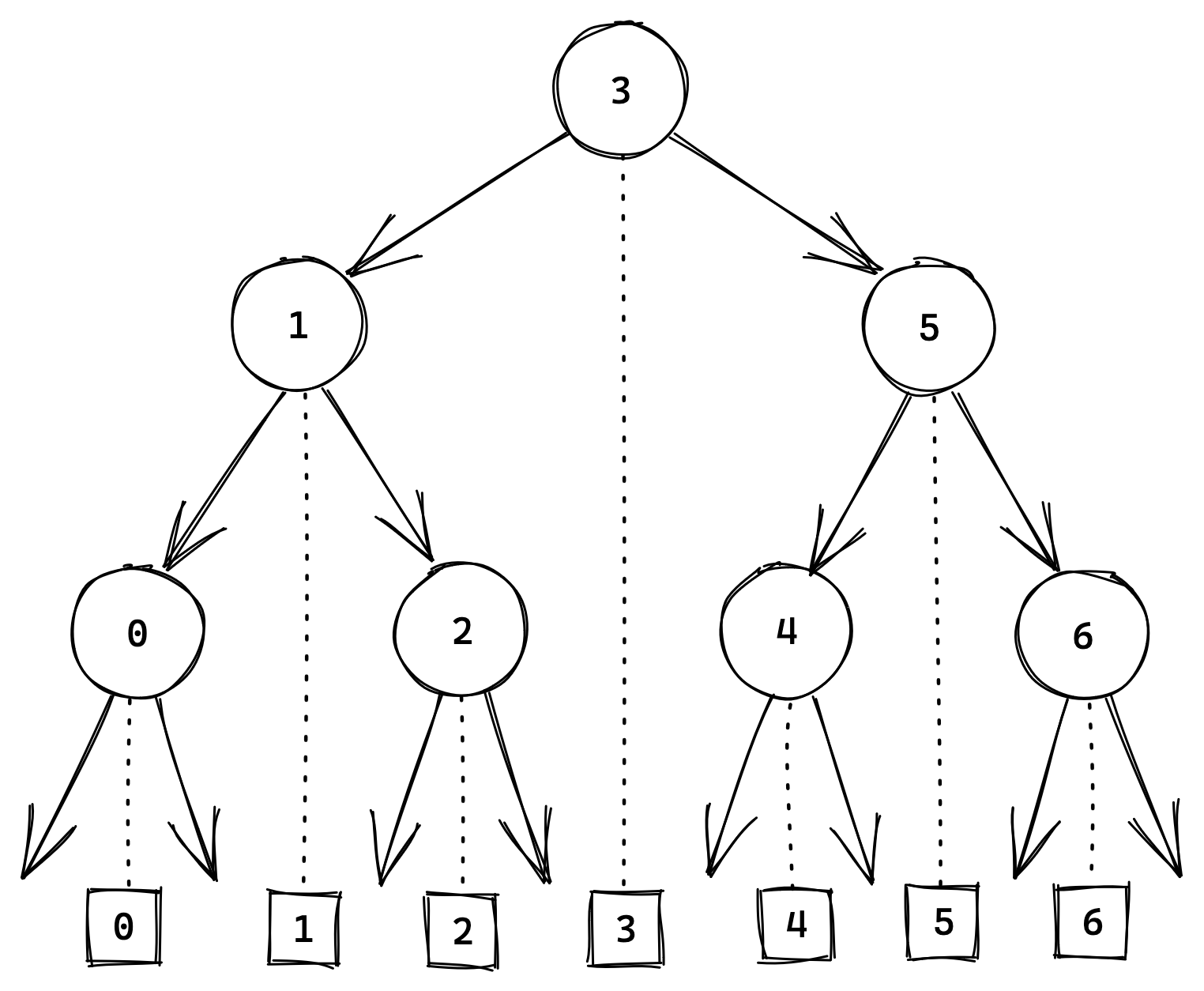
Thus the natural array size for binary search is $2^k - 1$, and not $2^k$.
A bitwise approach
Let’s take a look at the sixteen possible 4-bit integers in binary:
0 = 0000 8 = 1000
1 = 0001 9 = 1001
2 = 0010 10 = 1010
3 = 0011 11 = 1011
4 = 0100 12 = 1100
5 = 0101 13 = 1101
6 = 0110 14 = 1110
7 = 0111 15 = 1111
Notice how if the top bit of the integer is set, it remains set for all larger integers. And within each group with the same top bit, when the second most significant bit is set, it remains set for larger integers within that group. And so on for the third bit within each group with the same top two bits, ad infinitum. In binary, within each group with identical top $t$ bits set, the value of the $t+1$th bit is monotonically increasing.
Since our desired solution is the number of elements strictly less than $x,$ we can rephrase it as finding the largest number $b$ such that ${A[b-1] < x},$ or $b = 0$ if no elements are less than $x$. We can find the unique $b$ very efficiently by constructing it directly, bit-by-bit, using the above observation.
Let’s assume that $A$ has length $n = 2^k - 1$. Then any possible answer $b$ fits exactly in $k$ bits. Since $A$ is sorted, if we find that $A[i-1] < x$, we know that ${b \geq i}$. Conversely, if that comparison fails, we know that ${b < i}.$ Thus, using the above observation we can figure out if the top bit of $b$ is set simply by testing $A[i-1] < x$ with $i = 2^{k-1}$.
Now we know what the top bit should be and set it accordingly, never changing it again. Using the above observation, this time within the group of integers with a given top bit, we know that if we set the second bit and find that $A[i-1] < x$ still holds, that the second bit must be set, and if not it must be zero. We repeat this process bit-by-bit until we have figured out all bits of $b$, giving our answer!
Perhaps you are like me, and you are a visual thinker. Let us flip our earlier tree on its side and visually associate associate a binary $b$ value with each gap between the elements of our array:
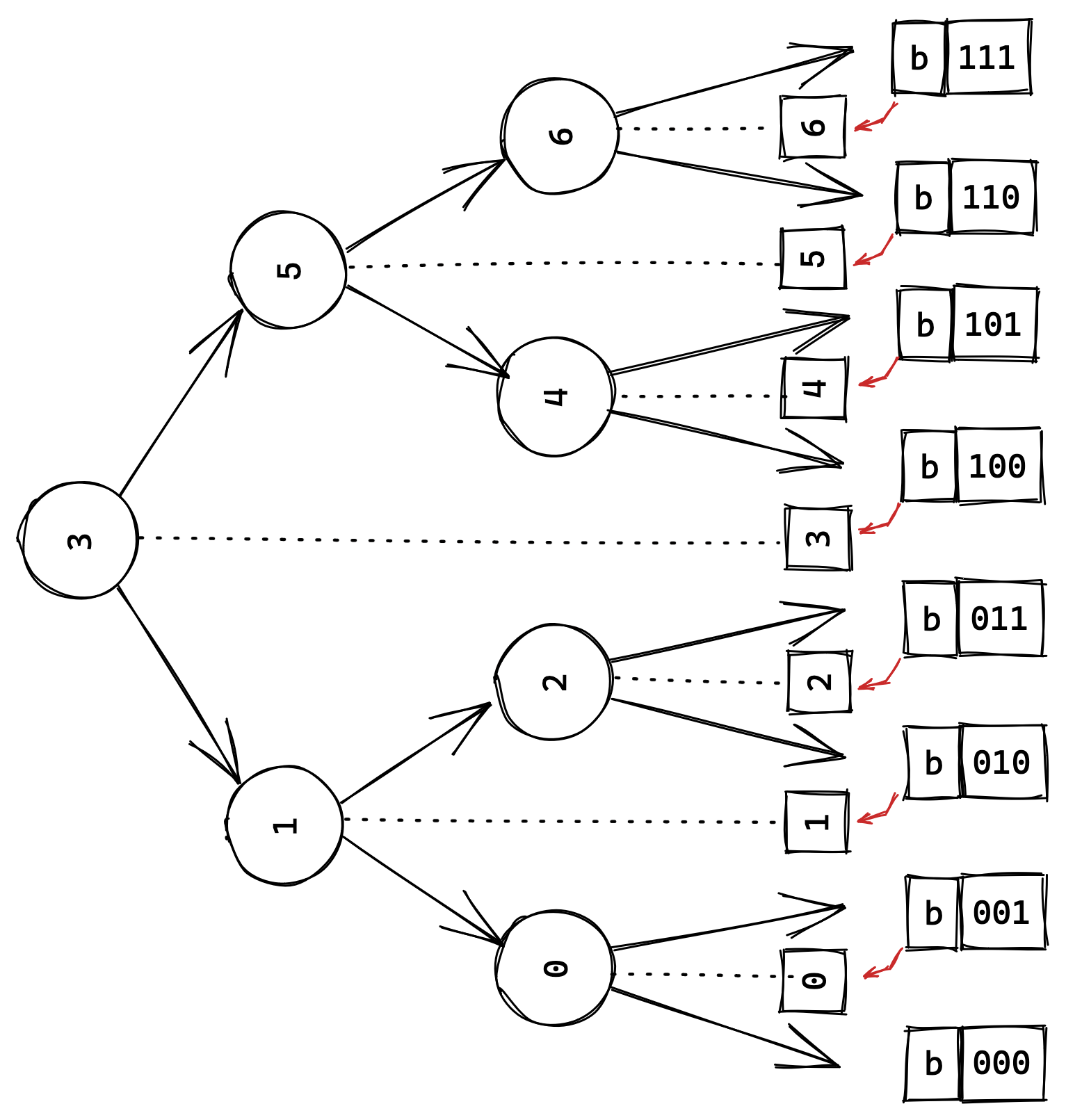
The small red arrows indicate which element $A[b-1] < x$ would test for a given guess of $b$. Note that no element is associated with $b = 0$, as we can only end up with this value if all other tests failed, and thus we never have to test this value. A search for $5$ would end up testing ${b = {\color{red}1}00_2}$ (success, set bit), ${b = 1{\color{red}1}0_2}$ (fail, do not set bit) and ${b = 10{\color{red}1}_2}$ (success, set bit).
In C++ we would get the following:
// Only works for n = 2^k - 1.
template<typename It, typename T, typename Cmp>
It lower_bound_2k1(It begin, It end, const T& value, Cmp comp) {
size_t two_k = (end - begin) + 1;
size_t b = 0;
for (size_t bit = two_k >> 1; bit != 0; bit >>= 1) {
if (comp(begin[(b | bit) - 1], value)) b |= bit;
}
return begin + b;
}
Note that we always do exactly $k$ comparisons, which is optimal.
Generalizing to other sizes
However, there is a glaring issue: our original array might not have length $2^k - 1$. The simplest way to solve this is to add elements with value $\infty$ to the end, to pad the array out to $2^k - 1$ elements. Instead of physically adding $\infty$ elements the array, we can simply check if the index lies in the original array, and if not skip our test entirely, as it would fail (we’d be testing if $\infty < x$).
To pad our array out we want to find the smallest integer $k$ such that $2^k - 1 \geq n$, which means $k \geq \log_2(n + 1)$, which after rounding up gives $$k = \lceil \log_2(n + 1) \rceil = \lfloor \log_2(n) \rfloor + 1.$$
Alternatively and definitely more enlightening is that this can be understood as
initializing bit in our loop to the highest set bit in $n$:
template<typename It, typename T, typename Cmp>
It lower_bound_pad(It begin, It end, const T& value, Cmp comp) {
size_t n = end - begin;
size_t b = 0;
for (size_t bit = std::bit_floor(n); bit != 0; bit >>= 1) {
size_t i = (b | bit) - 1;
if (i < n && comp(begin[i], value)) b |= bit;
}
return begin + b;
}
In my opinion this is the most elegant binary search implementation there is.
Making it branchless
The above works well, but introduces an index check before each array access. This means the compiler can not eliminate the branch here, lest we access out-of-bounds memory.
To solve this problem we use a similar trick as L. E. Shar: we do an initial comparison with the middle element, then either look at $2^k - 1$ elements at the start, or $2^k - 1$ elements at the end of the array. If the array size itself isn’t of the form $2^k - 1$, these two subslices overlap in the middle. To completely cover our array (together with the element we initially compare with) we must have $$(2^k - 1) + (2^k - 1) + 1 = 2^{k+1} - 1 \geq n$$ and thus we choose $k = \lceil \log_2(n + 1) - 1 \rceil = \lfloor \log_2 (n) \rfloor$ :
template<typename It, typename T, typename Cmp>
It lower_bound_overlap(It begin, It end, const T& value, Cmp comp) {
size_t n = end - begin;
if (n == 0) return begin;
size_t two_k = std::bit_floor(n);
if (comp(begin[n / 2], value)) begin = end - (two_k - 1);
size_t b = 0;
for (size_t bit = two_k >> 1; bit != 0; bit >>= 1) {
if (comp(begin[(b | bit) - 1], value)) b |= bit;
}
return begin + b;
}
Improving the efficiency
If our array doesn’t have size $2^{k+1} - 1$, the subarrays overlap in the middle. This means that part of the subarrays already eliminated by the initial comparison $A[n / 2] < x$ are being unnecessarily searched. Can we improve on this?
We can, if we choose two different sizes $2^l - 1$ and $2^r - 1$ for when we are respectively searching at the start (left) or end (right) of the array. Again, in combination with the initial element we compare with (which is now $A[2^l - 1] < x$) we find that we must have
$$(2^l - 1) + (2^r - 1) + 1 = 2^l + 2^r - 1 \geq n$$
to be able to handle an arbitrary size $n$. And of course, we must have $2^l - 1 \leq n$ and $2^r - 1 \leq n$ for our subarrays to fit. Let’s find the optimal choice for $l, r$—which is not trivial.
Cost analysis
What is the cost of a certain choice of $l, r$, assuming a uniform distribution over the $n + 1$ possible outcomes of the binary search? We know that after the initial comparison, for $2^l$ of those outcomes we use $l$ comparisons, and thus the rest must use $r$ comparisons for an expected cost of
$$C = 1 + \frac{2^l}{n + 1}\cdot l + \frac{n + 1 - 2^l}{n + 1}\cdot r$$
We only really care about minimizing this cost, so we can throw out the additional constant $+1$ and the factor $1/(n+1)$ as it does not change the relative order:
$$C’ = 2^l\cdot l + (n + 1 - 2^l)\cdot r$$
Optimizing $r$
Compare cost $C’$ to the expression $2^l \cdot l + 2^{r}\cdot r$. In this case the expression is entirely symmetrical, so we could freely swap $l$ and $r$. But we know from our earlier array size inequality that $n + 1 - 2^l \leq 2^{r}$. Thus we can conclude that $l$ has a greater weight in the cost than $r$ and therefore we can safely assume that $l \leq r$ is minimal.
From this plus the fact that $2^l + 2^{r} - 1 \geq n$ we can immediately deduce that $2^{r} \geq (n + 1) / 2$ by weakening the inequality with $2^l \to 2^r$, and thus rounding up to the nearest integer gives \begin{align*} r &= \lceil\log_2(n+1) - 1\rceil = \lfloor\log_2(n)\rfloor \end{align*}
Note that we can’t choose $r$ any larger, nor smaller, and thus we’ve determined the optimal value for $r$.
Optimizing $l$
Let’s reorder our relative cost $C’$ a bit:
$$C’ = 2^l\cdot (l - r) + (n + 1)\cdot r$$
We can ignore the second term as a constant, as we’re now trying to optimize $l$ given the optimal $r$. The function
$$f(l) = 2^x(l - r)$$ has derivative w.r.t. $l$ $$f’(l) = 2^l(\ln(2)(l - r) + 1)$$ with a single zero corresponding to the global minimum at $r - \frac{1}{\ln(2)} \approx r - 1.4427$. Let’s plug in the two integers closest to this minimum in $f$:
$$f(r - 1) = 2^{r - 1}(r - 1 - r) = - 2^{r-1}$$ $$f(r - 2) = 2^{r - 2}(r - 2 - r) = - 2^{r-1}$$
Thus we find that both $l = r - 1$ or $l = r - 2$ have optimal cost. For simplicity we can just limit ourselves to $l = r - 1$ as it is equal but easier to satisfy $2^l + 2^r - 1 \geq n$ with. Speaking of that inequality, we can’t always choose $l = r - 1$ as we are sometimes forced to choose $l = r$ by it.
Putting it together
We found that $r = \lfloor \log2(n) \rfloor$, and that
$$l = \begin{cases} r-1&\text{if }2^r + 2^{r-1} - 1 \geq n\\ r&\text{otherwise} \end{cases}.$$
The condition $2^r + 2^{r-1} - 1 \geq n$ can be seen to be equivalent to “the
$r-1$th bit of $n$ is not set”. And as $2^r - 2^{r-1} = 2^{r-1}$ we can isolate
that bit, negate it, and subtract it from two_r to get our two_l:
template<typename It, typename T, typename Cmp>
It lower_bound_opt(It begin, It end, const T& value, Cmp comp) {
size_t n = end - begin;
if (n == 0) return begin;
size_t two_r = std::bit_floor(n);
size_t two_l = two_r - ((two_r >> 1) & ~n);
bool use_r = comp(begin[two_l - 1], value);
size_t two_k = use_r ? two_r : two_l;
begin = use_r ? end - (two_r - 1) : begin;
size_t b = 0;
for (size_t bit = two_k >> 1; bit != 0; bit >>= 1) {
if (comp(begin[(b | bit) - 1], value)) b |= bit;
}
return begin + b;
}
The somewhat odd use of ternary statements and use_r is to convince the
compiler to generate branchless code. We certainly lost some of the elegance we
had before, but at least now we do the minimal number of comparisons we can do
with our bitwise binary search while being branchless. And it is in fact better
than than L. E. Shar’s original method, whose initial comparison $A[i - 1] < x$
uses $i = \left\lfloor \log_2 (n) \right\rfloor$, which is suboptimal as we’ve
seen.
Micro-optimizations
For some reason the standard implementation of
std::bit_floor… sucks
a bit. E.g. on x86-64 Clang 16.0 with
-O2 we compile this:
size_t bit_floor(size_t n) {
if (n == 0) return 0;
return std::bit_floor(n);
}
size_t bit_floor_manual(size_t n) {
if (n == 0) return 0;
return size_t(1) << (std::bit_width(n) - 1);
}
to this:
bit_floor(unsigned long):
test rdi, rdi
je .LBB0_1
shr rdi
je .LBB0_3
bsr rcx, rdi
xor rcx, 63
jmp .LBB0_5
.LBB0_1:
xor eax, eax
ret
.LBB0_3:
mov ecx, 64
.LBB0_5:
neg cl
mov eax, 1
shl rax, cl
ret
bit_floor_manual(unsigned long):
bsr rcx, rdi
mov eax, 1
shl rax, cl
test rdi, rdi
cmove rax, rdi
ret
Yikes. Manual computation it is!
Optimizing the tight loop
The astute observer might have noticed that in the following loop, we only
ever set each bit in b at most once:
size_t b = 0;
for (size_t bit = two_k >> 1; bit != 0; bit >>= 1) {
if (comp(begin[(b | bit) - 1], value)) b |= bit;
}
return begin + b;
This means we could change the binary OR to simple addition, which might optimize better in pointer calculations.
For the bitwise version we see the following tight loop for the above,
in x86-64 with GCC:
.L7:
mov rsi, rdx
or rsi, rcx
cmp DWORD PTR [rax-4+rsi*4], r8d
cmovb rcx, rsi
shr rdx
jne .L7
With addition we see the following:
.L7:
lea rsi, [rdx+rcx]
cmp DWORD PTR [rax-4+rsi*4], r8d
cmovb rcx, rsi
shr rdx
jne .L7
In fact, when using addition we could eliminate variable $b$ entirely,
and directly add to begin (similar to Skarupke’s original version that sparked
this article):
for (size_t bit = two_k >> 1; bit != 0; bit >>= 1) {
if (comp(begin[bit - 1], value)) begin += bit;
}
return begin;
However, I’ve found that some compilers, e.g. GCC on x86-64 will refuse to make
this variant branchless. I hate how fickle compilers can be sometimes, and I
wish compilers exposed not just the
likely/unlikely
attributes, but also an attribute that allows you to mark something as unpredictable
to nudge the compiler towards using branchless techniques like CMOV’s.
Instead of eliminating b, we can optimize the loop to only do a single addition
explicitly, by moving the -1 into the value of b itself:
size_t b = -1;
for (size_t bit = two_k >> 1; bit != 0; bit >>= 1) {
if (comp(begin[b + bit], value)) b += bit;
}
return begin + (b + 1);
Yay for two’s complement and integer overflow! This generated the best code on all platforms I’ve looked at, so I applied this pattern to all my implementations in the benchmark.
Results
Let’s compare all the variants we’ve made, both in comparisons and actual runtime. The latter I will test on my Apple M1 2021 Macbook Pro which is an ARM machine. Your mileage will vary on different machines, especially x86-64 machines, but I want this article to focus more on the algorithmic side of things rather than become an extensive study on the exact characteristics of branch mispredictions, cache misses, and how to get the compiler to generate branchless code for a variety of platforms.
The code for the below benchmark is available on my Github.
Comparisons
To test the average number of comparisons for size $n$ we can simply query for each of the $n + 1$ outcomes how many comparisons it takes to get that outcome. We then average over all these for a given $n$. The result is the following graph:
We see that lower_bound_opt does in fact do the fewest comparisons of
all the branchless methods, following the optimal lower_bound_std
more closely than lower_bound_pad or lower_bound_skarupke.
Across all sizes less than 256 we see the following average comparison counts, minus the optimal comparison count:
| Algorithm | Comparisons above optimal |
|---|---|
lower_bound_skarupke | 1.17835 |
lower_bound_overlap | 0.37250 |
lower_bound_pad | 0.17668 |
lower_bound_opt | 0.17238 |
lower_bound_std | 0.00000 |
All our hard work finding the optimal split into subarrays only saved us ~0.2
comparisons on average on lower_bound_opt versus the much simpler
lower_bound_overlap.
Runtime (32-bit integers)
To benchmark runtime for a certain size $n$ I pre-generated one million random integers in the range $[0, n + 1]$. Then I record the time it takes to look them all up using our lower bound routine of interest, and calculate the average.
Using clang 13.0.0 with g++ -O2 -std=c++20 we get the following:
I think this graph gives a fascinating insight into the branch predictor on the
Apple M1. Most striking is the relatively poor performance of lower_bound_opt.
Within each bracket of sizes $[2^k, 2^{k+1})$ it performs much worse
than lower_bound_overlap, with a size-dependent slope, before suddenly dropping to a
consistently good performance.
This puzzled me for a while, and I triple-checked to see that lower_bound_opt
was really being compiled with branchless instructions. Only then did I realize
there was a hidden branch all along: the loop exit condition.
lower_bound_overlap always performs the same number of loop iterations,
allowing the CPU to always correctly predict the loop exit, whereas
lower_bound_opt tries to reduce the number of iterations it does to save
comparisons. It turns out that for integers the cost of an extra iteration is
much lower than risking a mispredict on the loop condition on the Apple M1.
If we also look at larger inputs we see that the above pattern keeps up for quite a while until we start hitting sizes where cache effects become a factor:
We also note that it truly is important for a binary search benchmark to look at a variety of sizes, as you might reach rather different conclusions in performance at $n = 2^{12}$ versus $n = 2^{12} \cdot 1.5$.
A commonly heard advice is to not use binary search for small arrays, but to use a linear search instead. I find that not to be true on the Apple M1 for integers, at least compared to my branchless binary search, when searching a runtime-sized but otherwise fixed size array:
Note that a linear search must always incur at least one branch misprediction:
on the loop exit condition. For a fixed size array lower_bound_overlap has
zero branch mispredictions, including the loop exit.
Runtime (strings)
To benchmark the performance on strings I copied the above benchmark, except that I convert all integers to strings, zero-padded to a length of four. I also reduced the number of samples to 300,000 per size, as the string benchmark was significantly slower.
Using clang 13.0.0 with g++ -O2 -std=c++20 we get the following:
Strings are a lot less interesting than integers in this case, as most of the
branchless optimizations are moot. We find that initially the branchless
versions are only slightly slower than std::lower_bound due to the extra
comparisons needed. However once we get to the larger-than-cache sizes
std::lower_bound becomes significantly better as it can do speculative loads
to reduce cache misses.
It seems that for strings the advice to use linear searches for small input arrays doesn’t help that much, but doesn’t hurt either for $n \leq 9$, on the Apple M1.
Conclusion
In my opinion the bitwise binary search is an elegant alternative to the traditional binary search method, at the cost of ~0.17 to ~0.37 extra comparisons on average. It can be implemented in a branchless manner, which can be significantly faster when searching elements with a branchless comparison operator.
In this article we found the following implementation to perform the best on Apple M1 after all micro-optimizations are applied:
template<typename It, typename T, typename Cmp>
It lower_bound(It begin, It end, const T& value, Cmp comp) {
size_t n = end - begin;
if (n == 0) return begin;
size_t two_k = size_t(1) << (std::bit_width(n) - 1);
size_t b = comp(begin[n / 2], value) ? n - two_k : -1;
for (size_t bit = two_k >> 1; bit != 0; bit >>= 1) {
if (comp(begin[b + bit], value)) b += bit;
}
return begin + (b + 1);
}
However, when it comes to clarity and elegance I still find the following method the most beautiful:
template<typename It, typename T, typename Cmp>
It lower_bound(It begin, It end, const T& value, Cmp comp) {
size_t n = end - begin;
size_t b = 0;
for (size_t bit = std::bit_floor(n); bit != 0; bit >>= 1) {
size_t i = (b | bit) - 1;
if (i < n && comp(begin[i], value)) b |= bit;
}
return begin + b;
}